4차함수 비율관계 및 그래프 알아보자!

4차함수 비율관계 및 그래프에 대한 이야기는 수학적인 개념을 시각적으로 이해하는 데 도움이 되는 중요한 주제 중 하나입니다. 이 글에서는 4차함수와 관련된 비율관계와 그래프를 탐구하고 설명하겠습니다. 4차함수는 수학적으로 흥미로운 특성을 가지며, 그래프를 통해 이를 시각적으로 이해할 것입니다.
목차
1.4차함수의 개념
2.4차함수의 비율관계
3.4차함수 그래프의 특징
4.4차함수 그래프의 예시
5.4차함수의 활용
6.결론
1.4차함수의 개념
4차함수는 다음과 같이 나타낼 수 있습니다: f(x) = ax^4 + bx^3 + cx^2 + dx + e, 여기서 a, b, c, d, e는 상수입니다. 이 함수는 x의 4승에 대한 다항식이며, x에 대한 최고차항이 4차인 함수입니다. 4차함수는 기본적인 다항 함수 중 하나로, 여러 영역에서 중요한 역할을 합니다.


2.4차함수의 비율관계
4차함수의 비율관계는 함수의 계수에 따라 그래프의 형태가 어떻게 변하는지를 나타냅니다. 예를 들어, a가 양수일 때 그래프는 오른쪽 위로 향하고, a가 음수일 때 그래프는 오른쪽 아래로 향합니다. b, c, d, e의 값도 그래프의 모양을 조절합니다. 비율관계를 이해하면 함수의 특성을 예측하고 그래프를 분석하는 데 도움이 됩니다.
3.4차함수 그래프의 특징
4차함수의 그래프는 대칭성을 가집니다. 그래프의 중심이 (0, 0)에 위치하며, 이를 중심에 대칭된 형태로 그려집니다. 그래프는 두 개의 극소점을 가지며, 그 꼭짓점에서 방향을 바꿉니다. 이러한 특징은 함수의 비율관계와 관련이 깊습니다.
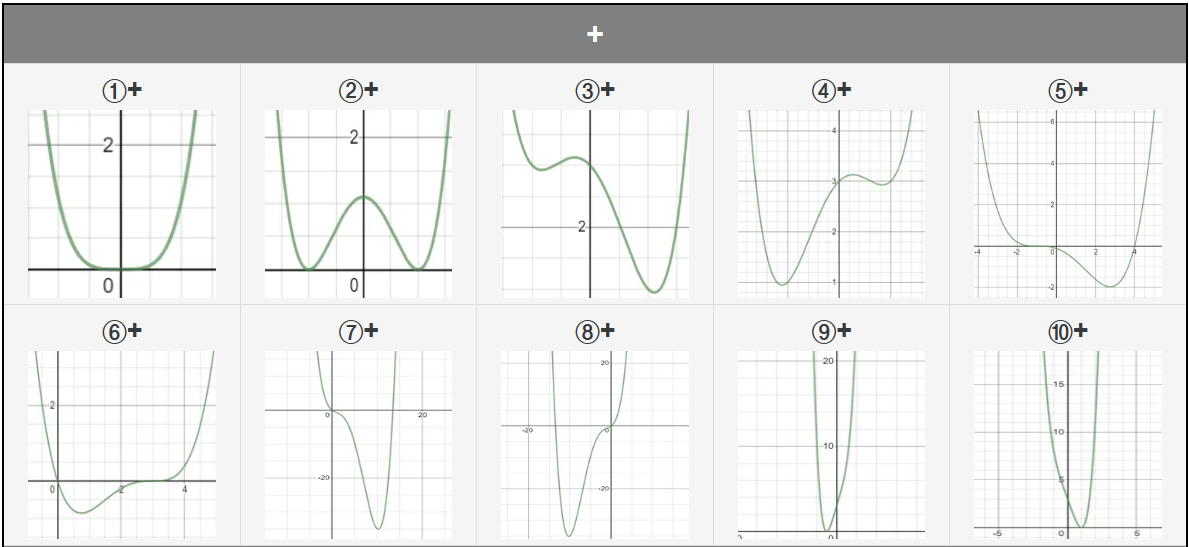
4.4차함수 그래프의 예시
아래는 몇 가지 4차함수 그래프의 예시입니다.
f(x) = x^4: 이 함수는 x=0에서 최솟값을 갖고 대칭적인 그래프를 가집니다.
f(x) = -2x^4 + 3x^2: 이 함수는 x=0에서 최댓값을 갖고 대칭적이지만 아래로 볼록한 그래프를 가집니다.
f(x) = 4x^4 - 8x^3 + 4x^2: 이 함수는 x=1에서 극대값을 가집니다.

5.4차함수의 활용
4차함수는 다양한 분야에서 활용됩니다. 물리학, 공학, 경제학 등 다양한 분야에서 현상을 모델링하거나 데이터를 분석할 때 사용됩니다. 또한, 4차함수의 비율관계를 이해하면 복잡한 문제를 간단하게 해결하는 데 도움이 됩니다.
6.결론:
4차함수와 그래프는 수학적인 개념을 시각적으로 이해하는 데 중요한 역할을 합니다. 이 글에서는 4차함수의 개념, 비율관계, 그래프의 특징, 예시, 그리고 활용에 대해 다뤘습니다. 4차함수는 다양한 분야에서 활용되며, 그 그래프를 통해 수학적인 문제를 해결하는 데 도움이 됩니다. 수학을 더 깊이 탐구하고 싶다면 4차함수를 공부하는 것을 고려해보세요.
4차함수와 그래프는 수학의 중요한 부분 중 하나로, 이해하고 활용하는 것은 수학 능력뿐만 아니라 다른 분야에서의 문제 해결 능력을 향상시키는 데 도움이 됩니다. 이 글에서 다룬 주제는 4차함수의 기초적인 이해와 시각적 표현에 초점을 맞추었지만, 이를 더 깊게 탐구하고 다양한 응용 분야에서 활용할 수 있습니다.

4차함수와 관련된 학습은 수학적 직관을 키우고, 문제 해결 능력을 강화하는 중요한 요소입니다. 더 나아가, 4차함수는 현실 세계의 다양한 현상을 모델링하는 데 사용되며, 데이터 과학, 엔지니어링, 경제학 등의 분야에서 핵심적인 역할을 합니다.
이러한 이해와 활용을 통해 수학은 단순히 수학 시험을 위한 도구가 아니라, 현실 세계에서의 문제 해결과 창의적 사고를 촉진하는 도구로서의 가치를 확인합니다. 따라서 4차함수와 그래프에 대한 학습은 미래에도 계속하여 유용하고 중요한 것입니다. 수학을 통해 세계를 더 깊이 이해하고, 문제를 해결하는 과정에서 성장하실 수 있을 것입니다.
감사합니다.

'폰지킬러's 생활 속 꿀팁 이야기' 카테고리의 다른 글
| 귓바퀴 통증, 염증 및 귀 부음 알아보자! (0) | 2023.10.26 |
|---|---|
| 바나나 효능 및 보관법 알아보자! (2) | 2023.10.25 |
| 겨울 여행지 추천 알아볼게요! (0) | 2023.10.20 |
| 수면 무호흡증 증세 및 치료 방법 알아보자! (0) | 2023.10.20 |
| 피망 파프리카 차이: 맛과 특징을 자세히 알아보기! (0) | 2023.10.18 |